Um dos temas mais cobrados em provas é estatística e probabilidade. Então, veja neste artigo como esses temas mais aparecem. Em primeiro lugar é essencial ressaltar que a variância e os desvios são medidas de dispersão.
Já as mais importantes medidas de tendência central são: média aritmética, média aritmética ponderada, mediana, moda, média geométrica, média harmônica e quartis.
No entanto, quando estudamos a variabilidade das medidas, consequentemente chegamos aos desvios e à variância. Desta forma, para medir a variação presente num conjunto de dados utilizamos a variabilidade, assim como a dispersão desses dados. Outrossim, relativamente na medida de localização do centro da amostra do conjunto.
Certamente, sendo a média a medida de localização mais importante, será relativamente a ela que se define a principal medida de dispersão: a variância, apresentada a seguir.
O que é a variância?
É a medida que se obtém quando somamos os quadrados dos desvios da observação da amostra, em relação a sua média, assim como, dividimos pelo número de observações da amostra menos um.
Sendo:
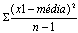
O que é o desvio-padrão?
Assim, sendo que a variância envolve a soma de quadrados, a sua unidade não é a mesma dos dados. Além disso, o desvio padrão é obtido através da raiz quadrada da variância para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados.
Em resumo, o desvio padrão precisa ser positivo, não podendo assumir valores negativos. Certamente quanto maior for o seu valor, maior será a dispersão dos dados.
Sendo:
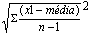
Assim, com a utilização dessas medidas, é possível se ter uma noção mais aproximada das médias do conjunto estudado. Por exemplo, em um exame onde se avalia o candidato pela média de acertos, para saber como se saiu basta o candidato se comparar ao número de acertos dos demais concorrentes.
No entanto se, por exemplo, a entidade que realizou a prova deseja fazer uma atividade de reforço para os candidatos que obtiveram um média abaixo de 6,0, por exemplo, será necessário obter mais informações sobre esses candidatos em específico, para que seja possível auxiliá-los.
Teste seus conhecimentos
Então, para o nosso exercício, vamos considerar o seguinte conjunto de informações:
| X | Y | Z | |
| 1 | 1 | 2 | 4 |
| 2 | 2 | 4 | 5 |
| 3 | 3 | 6 | 6 |
| 4 | 4 | 8 | 7 |
| 5 | 5 | 10 | 8 |
Assim, para cada uma das variáveis apresentadas (X, Y e Z), calcule a variância e também o desvio padrão.
Resolução do exercício, variável “Y”

Importante: Perceba que neste caso estamos calculando os valores referentes à variável “Y”. Do mesmo modo, deverá ser realizado o mesmo com as outras variáveis.
Outra questão importante no tema estatística e probabilidade é que, embora o enunciado solicite apenas o cálculo da variância e do desvio padrão, neste caso se faz necessário calcularmos a média, em razão de que ela será necessária para os demais cálculos realizados.
Resultado final do exercício
| Variável | Média | Variância | Desvio Padrão |
| X | 3 | 2,5 | 1,58 |
| Y | 6 | 10 | 3,16, |
| Z | 6 | 2,5 | 1,58 |
Dicas Enem
Então, se você está buscando melhorar seus conhecimentos para aumentar suas chances para a próxima prova do Enem e, da mesma forma, conseguir boas referências nas notas de corte.
Assim, nossa sugestão é que você estude todos os assuntos de Matemática disponíveis aqui no Guia de Ensino. Certamente, uma boa preparação na prova de Exatas pode lhe auxiliar a alcançar aquela nota tão desejada.
Estude ainda mais:
- Medidas de Tendência Central;
- Estatística e probabilidade: representação e análise de dados;
- Operações em conjuntos numéricos (naturais, inteiros, racionais e reais).
Assim, não deixe de estudar e boa sorte!


