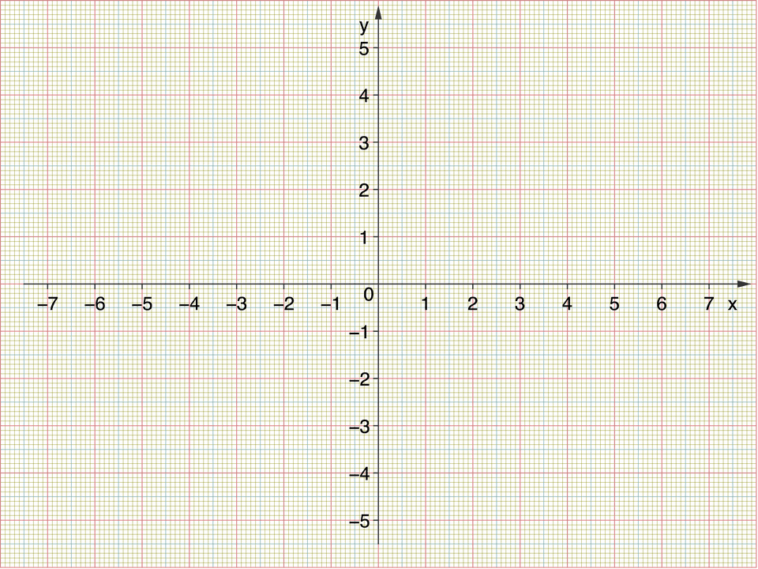
Criado pelo matemático e filósofo francês, René Descartes, o sistema de coordenadas cartesianas ou plano cartesiano é um método de localização de pontos. Esse sistema é composto por duas retas perpendiculares entre si.
A reta no eixo horizontal é chamada de abscissa e tem como representação a letra X. Enquanto isso, o eixo na vertical recebe a denominação de ordenada, sendo retratada pela letra Y. Vejo um exemplo de plano cartesiano abaixo:
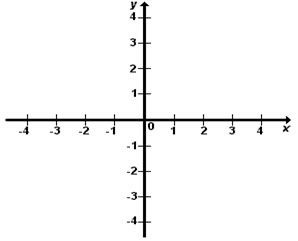
Os eixos do plano cartesiano são enumerados com os algarismos que compõem o conjunto dos números reais. Além disso, o ponto de encontro entre as duas retas é denominada de origem, pois marca o ponto zero de ambas as retas.
Dessa forma, para localizar um ponto no plano cartesiano é preciso utilizar as coordenadas cartesianas. Essa coordenada é composta por um ponto no eixo X e um no eixo Y, sempre nessa ordem (X,Y).
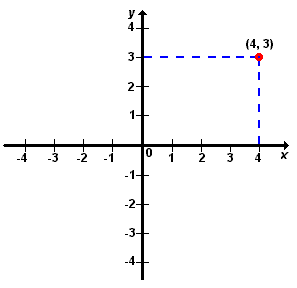
Por conta disso, recomenda-se localizar primeiro a posição do ponto no eixo X e posteriormente no eixo Y. Veja o exemplo do par de coordenadas (4,3):
Quadrantes do plano cartesiano
Por serem retas perpendiculares, os eixos das abscissas e das ordenadas criam quatro quadrantes diferentes.
Além disso, por serem enumerados pelo conjunto dos números reais, os algarismos dos eixos podem ser negativos ou positivos.
Dessa forma, cada quadrante possui uma particularidade em relação às coordenadas. Veja os quadrantes:
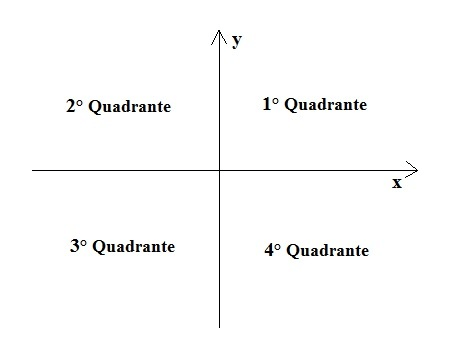
Sabendo que os números positivos crescem para direita e para cima, a partir da origem, e os números negativos vão para esquerda e para baixo, temos:
- 1° Quadrante → Os números dos dois eixos sempre será positivo com o X e o Y sendo maior que 0.
- 2° Quadrante → O número do eixo das abcissas sempre será negativo com o X menor que 0. Enquanto isso, o número do eixo das ordenadas sempre será positivo com o Y maior que 0.
- 3° Quadrante → Os números dos dois eixos sempre será negativo com X e o Y sendo menores que 0.
- 4° Quadrante → O número do eixo das abscissas sempre será positivo com o X maior que 0. Enquanto isso, o número do eixo das ordenadas sempre será negativo com o Y menor que 0.
Dicas Enem
Para você que vai prestar o Enem, fique atento ao plano cartesiano e as suas funcionalidades pois eles são usados em diversos exercícios da prova, como no exemplo abaixo:
(Enem – 2016) Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
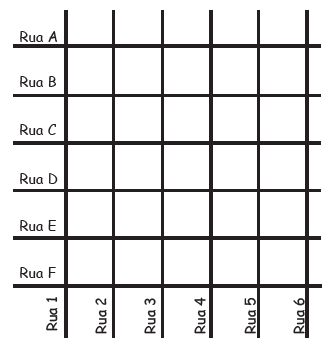
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
A) 3 e C.
B) 4 e C.
C) 4 e D.
D) 4 e E.
E) 5 e C.
Resolução:
Como os locais de trabalho do mãe e do pai se localizam na rua E, o imóvel deverá ser localizado na rua 4, que é a mediatriz dos pontos correspondentes.
A distância do consultório até a escola é de 6 quarteirões, logo o imóvel deverá ser situado a três quarteirões de cada. Com isso, o imóvel deve ser instalado no encontro das ruas 4 e D.
Resposta certa: Letra C.
Em suma, o plano cartesiano é uma ótima alternativa para realizar a localização de diferentes pontos. Além disso, é necessário seguir a ordem de primeiro o número do eixo das abscissas e o segundo número do eixo das ordenadas, sendo (X,Y).