Geometria é uma ciência que é parte da matemática, que tem como objetivo estudar o espaço e as figuras que podem ocupá-lo. Hoje em dia, já há uma ciência mais aprofundada que busca visualizar essas figuras geométricas na natureza e também nas construções feitas pelo humano.
As três entidades fundamentais da Geometria das quais surgem quase todas as figuras geométricas são:
- ponto
- reta
- plano
São, então, entes primitivos, não possuem definição. Suas representações são dadas pelos seguintes desenhos:
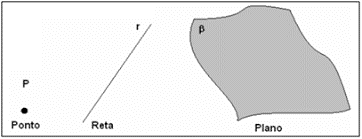
Reta e ponto
As retas são infinitas, mas podem nomear um ponto nela, utilizando letras maiúsculas, e essa será a notação. Pode-se também nomear a reta, que sempre vai em ambas as direções, com letra minúscula.
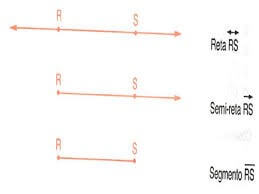
Há também a semirreta, quando possui um ponto finito de origem, mas segue para um sentido infinito. Enquanto a semirreta que possui origem e fim recebe o nome de segmento de reta.
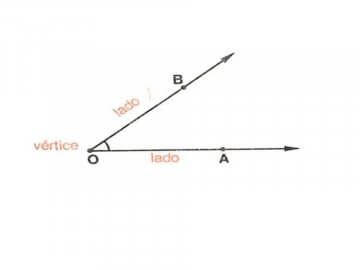
Ângulo e lado
Podemos visualizar alguns outros elementos nessas formas geométricas e espaciais.
O ângulo é a parte do plano delimitada por duas semirretas de mesma origem. Chamam-se de lado as duas semirretas que formam o ângulo e de vértice a origem comum às duas semirretas.
Na escrita, pode-se representar esse ângulo de três modos mais comuns:
- Com n notação dos três pontos: ângulo AÔB ou ângulo BÔA;
- Com a notação do vértice do ângulo: ângulo Ô;
- Ou por meio de sua medida: ângulo α.
Somente a respeito destas características, os ângulos, há um grande estudo de classificação, operacionalização, relação entre eles e unidades de medida, que não vamos aprofundar aqui. O Teorema de Tales, por exemplo, surge deste estudo.
Circunferência e círculo
A roda de um automóvel é um círculo ou uma circunferência? Os planetas movimentam-se ao redor do Sol de modo circular ou elipsoidal? Por mais estranho que isso possa parecer, esses elementos estão presentes no dia a dia.
O conjunto de pontos do plano situado à mesma distância de um ponto fixo forma uma circunferência. O ponto fixo é chamado de centro.
Uma circunferência possui os seguintes elementos:
- raio (segmento que une o centro a qualquer ponto da circunferência)
- corda (qualquer segmento de reta cujas extremidades estão sobre a circunferência)
- diâmetro (corda máxima que passa necessariamente pelo centro da circunferência. Sua medida é o dobro da medida do raio)
- arco (parte da circunferência compreendida entre dois de seus pontos)
O círculo é toda região interna da circunferência, inclusive a própria linha de contorno. É, portanto, a região do plano delimitada por uma circunferência.
Triângulos
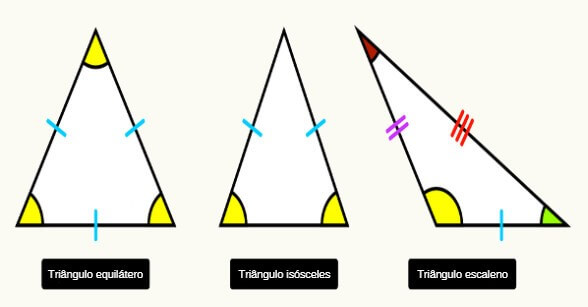
Essa é das principais figuras geométricas utilizadas na engenharia e na arquitetura. A definição de um triângulo é a união dos segmentos formados por três pontos distintos e não-colineares do plano, ou seja, não alinhados na mesma reta.
Novamente, não vamos aprofundar o estudo dessa forma específica, mas há duas propriedades gerais que podemos citar:
1- Em todo triângulo, o lado de maior medida sempre se opõe ao ângulo de maior medida e o lado de menor medida sempre se opõe ao ângulo de menor medida;
2- Desigualdade triangular: a medida de um dos lados do triângulo é sempre menor que a soma das medidas dos demais lados.
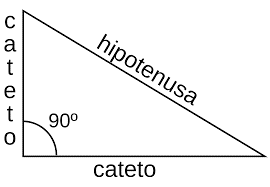
Entre os tipos de triângulos existentes, está o de ângulo reto, o triângulo retângulo, que possui elementos específicos definidos, basicamente, como o cateto e a hipotenusa, sendo o cateto os lados de um ângulo reto e a hipotenusa o lado oposto.
Polígonos
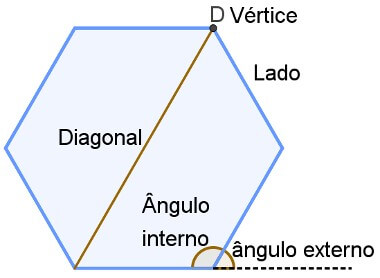
Uma linha poligonal, ou seja, uma sucessão de segmentos de retas consecutivas e não-colineares é chamada de linha poligonal, formando um polígono. Toda a região interna a esse polígono, inclusive a linha poligonal, recebe o nome de região poligonal ou superfície poligonal.
Nessa forma, como em todas as outras, há lados, ângulos internos e externos (ângulo formado pelo prolongamento de um lado e seu lado consecutivo).
Além disso, podemos também traçar um novo segmento nessa forma, e também no quadrilátero chamado de diagonal, ou seja, que liga dois vértices não consecutivos.
Quadrilátero
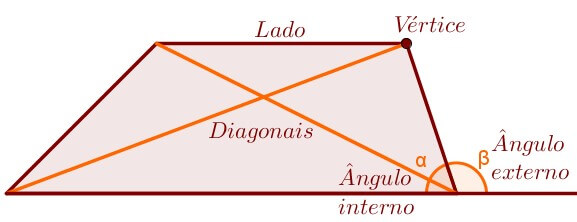
Um polígono que possui quatro lados é chamado de quadrilátero. Possui, então, os mesmos elementos de observação e análise, com algumas particularidades padrão.
Por exemplo, o teorema da soma dos ângulos internos, ou seja, a propriedade de que a soma dos ângulos internos de qualquer quadrilátero sempre formará um ângulo giro, ou de volta completa, e então a soma de suas medidas é sempre igual à 360°.
Assim como todas as outras formas geométricas podemos, por exemplo, fazer o estudo da área da superfície, traçar relações entre as retas, distâncias, entre outras, que geram equações matemáticas.
São ferramentas bastante utilizadas, por exemplo, para desenhar mapas e escalas. Além disso, é possível estudar também os vetores existentes no plano e também movimentos, rotações, translações e reflexões.
Figuras espaciais
A arte contemporânea surgiu logo após a Segunda Guerra Mundial, em meados da década de 1940, e o uso da matemática com fins expressivos foi significativa. É por isso que vemos nas construções, não só atuais, como também antigas, tantas formas geométricas em suas diferentes precisões.
O poliedro seria a representação base de todas as figuras espaciais, ou seja, com três dimensões, que é a nossa realidade base – sem adentrar aqui às pesquisas mais modernas das ciências exatas. É, portanto, um espaço com volume.
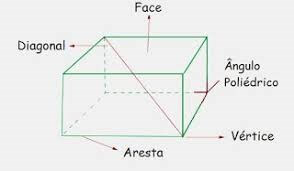
Um poliedro e um sólido geométrico delimitado por quatro ou mais polígonos. Os polígonos que limitam um poliedro são chamados de faces e seus lados e vértices são denominados, respectivamente, arestas e vértices. Abaixo, alguns dos tipos de poliedros existentes:


Prisma
O prisma óptico é um instrumento bastante utilizado em experimentos no campo da Física. Com ele, é possível dividir a luz nas cores que compõem o espectro da luz solar, também conhecida como arco-íris.
Geometricamente, é qualquer poliedro que possui duas faces congruentes, paralelas e convexas, denominadas vases, e cujas faces restantes são paralelogramos, denominados faces laterais.
Pirâmide
Não se sabe ao certo por qual motivo as pirâmides foram construídas com a forma que foram.
Há hipóteses levantadas pelos milhares de pesquisadores do passado e presente, a questão é que se trata de uma das mais importantes construções que já existiram.
Assim, os egípcios foram pioneiros. Há também algumas questões misteriosas, que chamam muita atenção dos estudiosos.
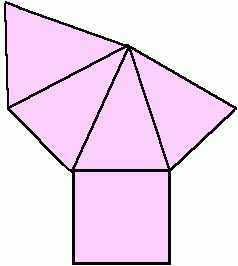
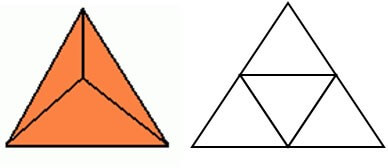
Entre outras infinitos objetivos e objetos de estudo, há a possibilidade, por exemplo, de planificar as formas espaciais volumosas. A planificação de um tronco de uma pirâmide reto é formada pelos polígonos das bases e pelos trapézios isósceles congruentes.
Cilindros
No dia a dia vemos muito essa forma. É o que vemos em uma latinha de refrigerante, por exemplo, ou no eixo de um carro.
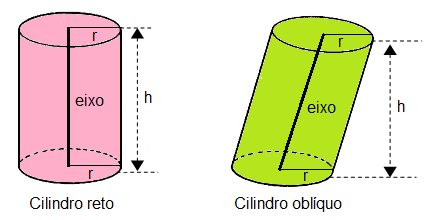
Um corpo redondo que possui duas fases circulares, congruentes e paralelas, denominadas bases, e uma superfície nomeada superfície lateral, arredondada, que pode ser planificada, é chamada de cilindro.
Por ter essa forma, possui os elementos: bases, raio, eixo, geratriz e altura.
Cone
Quem nunca plantou uma muda de flor? O vaso é equivalente à um tronco de um cone. Completo, ele se parece mais com a casquinha do sorvete.
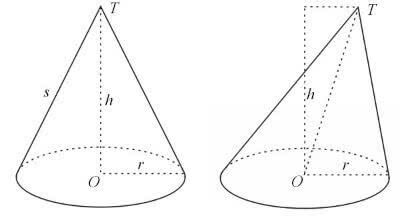
Geometricamente falando, quando se reúnem todos os segmentos de reta formados entre os pontos de um círculo e um ponto V fora dele, forma-se um corpo redondo chamado de cone.
Assim como o cilindro, também possui base, vértice, altura, eixo e giretriz. E também pode ser reto um oblíquo.
O cone reto também pode ser chamado de cone de revolução, pois pode ser obtido rotacionando um triângulo retângulo ao redor de um de seus catetos.
Esfera
O melhor exemplo para mostrar o que é a esfera seria a esfera terrestre, o globo do nosso Planeta Terra.
Geometricamente, a esfera é um corpo redondo composto pelos pontos do espaço que equidistam de um ponto fixo O, e de todos os seus pontos interiores.
Ela pode ser obtida rotacionando-se um semicírculo sobre um eixo que passa pelo seu diâmetro. Seus principais elementos são o raio e o centro, além do volume, é claro.
Dicas Enem
As figuras geométricas são cobradas em vários tipos de vestibulares. Portanto, releia o artigo acima e aprofunde seus estudos sobre as principais figuras geométricas. Continue acompanhando nosso blog!


