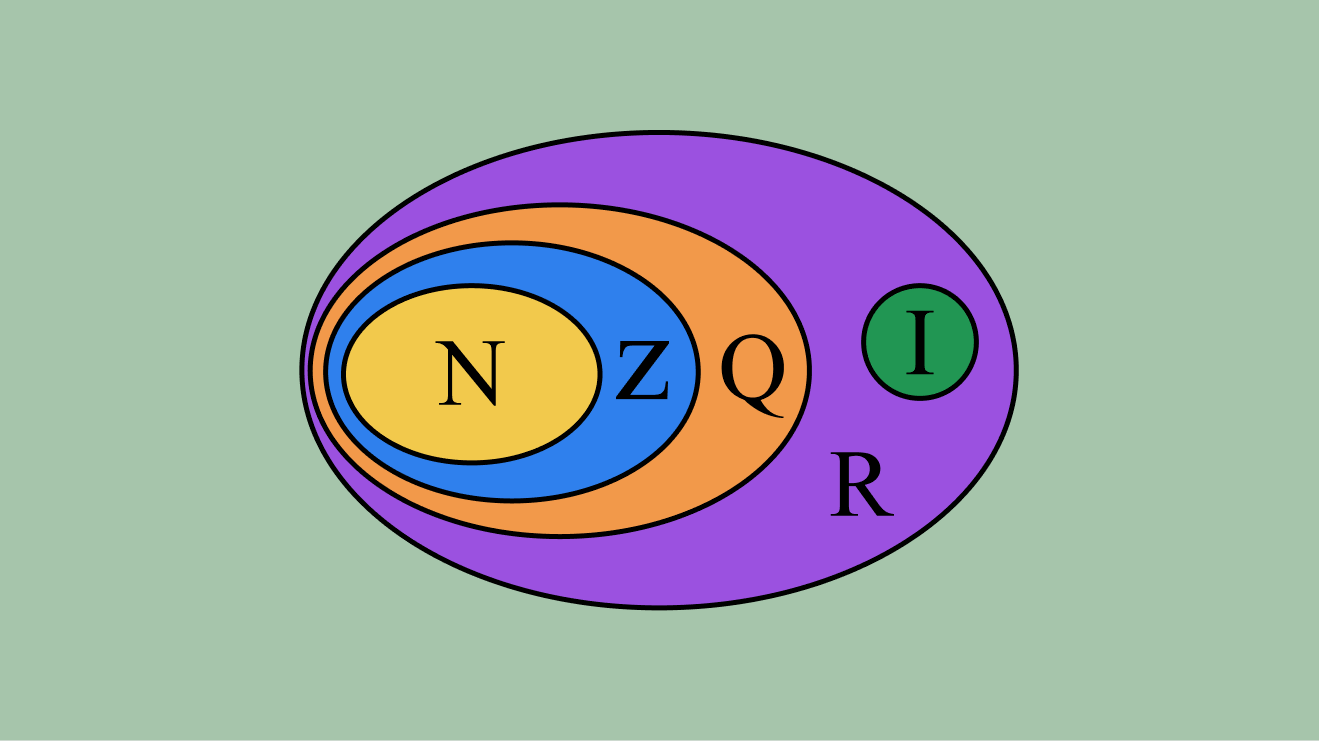
Em primeiro lugar é importante sabermos que as operações em conjuntos numéricos, reúnem vários conjuntos distintos de números. Sendo eles formados por números naturais, inteiros, racionais e reais. Vamos conhece-los?
Operação em Conjunto de Números Naturais
As operações do conjunto dos números naturais e representada na matemática pela letra “N”. Sendo que, esse conjunto reúne todos os números que utilizamos para contar, iniciando em zero até o infinito. No entanto é possível se obter a representação de apenas de seus subconjunto.
Subconjuntos dos Números Naturais
- N* = {1, 2, 3, 4, 5…, n, …} ou N* = N – {0} – É o conjunto dos números naturais não-nulos, ou seja, sem o zero.
- P = {2, 3, 5, 7, 11, 13, …} – É o conjunto dos números naturais primos.
- Np = {0, 2, 4, 6, 8…, 2n, …}, onde n ∈ N – É o conjunto dos números naturais pares.
- Ni = {1, 3, 5, 7, 9…, 2n+1, …}, onde que n ∈ N – É o conjunto dos números naturais ímpares.
Operação do Conjunto dos Números Inteiros
As operações do conjunto dos números inteiros, são representadas na matemática pela letra “Z”. Esses conjuntos reúnem todos os elementos dos números naturais e seus opostos. Ou seja, cada um dos números naturais possui um oposto. O oposto do 1 é o -1, do 2 o -2 e assim por diante. Apenas com a exceção do zero.
Subconjuntos dos Números Inteiros
- Z* = {…, –4, –3, –2, –1, 1, 2, 3, 4, …} ou Z* = Z – {0} – São os conjuntos dos números inteiros não-nulos, em consequência, sem o zero.
- Z+ = {0, 1, 2, 3, 4, 5, …} –É o conjunto dos números inteiros não-negativos.
- Z*+ = {1, 2, 3, 4, 5, …} – É o conjunto dos números inteiros positivos, sem o zero.
- Z – = {…, –5, –4, –3, –2, –1, 0} – É o conjunto dos números inteiros não-positivos.
- Z*– = {…, –5, –4, –3, –2, –1} – É o conjunto dos números inteiros negativos e sem o zero.
Operação do Conjunto dos Números Racionais
As operações do conjunto dos números racionais é representada na matemática pela letra “Q”. Sendo que, são os conjuntos que reúne todos os números que podem ser escritos na forma p/q. Em outras palavras, são aqueles números que podem ser expressos através de frações.
É importante ressaltar, que todo o número inteiro, também é um número racional.
Q = {0, ±1, ±1/2, ±1/3, …, ±2, ±2/3, ±2/5, …, ±3, ±3/2, ±3/4, …}
Subconjuntos dos Números Racionais
- Q* – Números racionais não-nulos, em suma, formado pelos números racionais sem o zero.
- Q+ – Números racionais não-negativos, em suma, formado pelos números racionais positivos e o zero.
- Q*+ – Números racionais positivos, em suma, formado pelos números racionais positivos, sem o zero.
- Q– = Números racionais não-positivos, em suma, formado pelos números racionais negativos e o zero.
- Q*– = Números racionais negativos, em suma, formado números racionais negativos, sem o zero.
Operações do Conjunto dos Números Irracionais
A operação do conjunto dos números irracionais é representado na matemática pela letra “I”, e por sua vez reúne os números decimais não exatos com uma representação infinita e não periódica.
Operações do Conjunto dos Números Reais
Por sua vez, as operações do conjunto dos números reais é representada na matemática pela letra “R”, sendo formada pela união dos números racionais e irracionais.
Dicas Para o ENEN
Então, se você que está se preparando para o ENEN, primeiramente gostaria de lhe desejar boa sorte. Em segundo lugar, saiba que a prova de matemática do exame é decisiva para uma boa nota. Então, em resumo, não deixe de conferir outros post do guia de ensino.
Confira também:
- Estatística e probabilidade: representação e análise de dados
- Grandezas, unidades de medida e escalas
Exercício Resolvido
Um professor de matemática, ao lecionar a Teoria dos Conjuntos em uma turma. Sendo assim, realizou uma pesquisa sobre as preferências clubistas de seus alunos, tendo chegado ao seguinte resultado:
- 23 Alunos torcem para o Paysandu;
- 23 Alunos torcem para o Remo;
- 15 Alunos torcem para o Vasco;
- 6 Alunos torcem para o Paysandu e para o Vasco
- 5 Alunos torcem pelo Vasco e pelo Remo
Desta forma, se designarmos por um A o conjunto dos torcedores do Paysandu, por um B o conjunto dos torcedores do Remo e por C o conjunto dos torcedores do Vasco, todos da referida turma. Concluímos que o número de aluno dessa turma é:
a) 49
b) 50
c) 47
d) 45
e) 46
Resposta correta: “b”