Certamente, é comum quando estamos estudando alguma questões matemáticas nos questionarmos da aplicabilidade das fórmulas. Afinal, quem nunca se perguntou: para que eu uso isso? Então, saiba que a função algébrica do 2º grau é muito utilizada em nosso cotidiano.
Por exemplo, as áreas de engenharia, utilizam constantemente essas fórmulas. Mas não somente na engenharia. Por exemplo: se você deseja seguir a carreira de administrador precisará da função algébrica de 2º grau para calcular as receitas e lucros da empresa. Certamente, é muito importante conhecer essas fórmulas matemáticas. Então, vamos lá?
Conceito de função algébrica de 2º grau
A Função Polinomial do 2° Grau também é conhecida como Função Quadrática. Ela é uma função real definida por: f(x) = ax2 + bx + c na qual a, b e c são coeficientes reais, sendo a ≠ 0.
Sendo que toda equação de 2º grau pode ser escrita de forma reduzida, como: ax² + bx + c = 0, uma vez que são definidas na incógnita X.
Neste caso, a, b e c são considerados números reis, sendo obrigatório que eles sejam diferente de zero. Onde:
- a é o coeficiente de x²;
- b é o coeficiente de x;
- c é o termo independente.
Podendo, portanto, ser representado da seguinte forma:
2x² + 3x – 5 = 0
Onde:
- O coeficiente a é 2;
- O coeficiente b é 3
- O termo independente c é -5
Representação gráfica
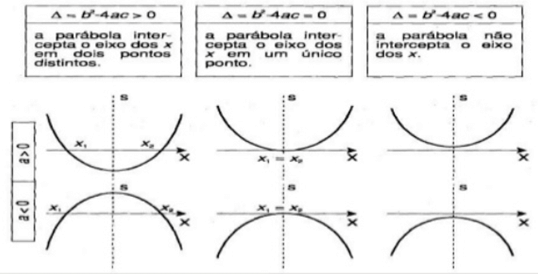
Da mesma forma, o gráfico da função de 2º grau é apresentado em forma de U, ou seja, com característica de parábola. Em suma, toda a parábola é simétrica em relação a um eixo. Este eixo, por sua vez, é chamado de simetria ou eixo da parábola.
E concluindo, o ponto onde a parábola intercepta o eixo é conhecido como vértice.
Por exemplo:
Construção do gráfico da função: y = x² + x
Primeiramente, atribuímos a x alguns valores, depois calculamos o valor correspondente de y. Na sequência ligamos os pontos obtidos.
Sendo assim, então:
- Se a>0, a parábola tem a concavidade voltada para cima;
- Se a< 0 a parábola tem a concavidade voltada para baixo;
O gráfico será representado da seguinte forma:
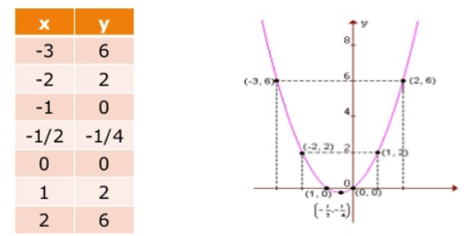
Representação gráfica da função de 2º grau (Fonte: Prof.: Cristiane Borges)
Exercício resolvido
Então vamos praticar? Abaixo apresentamos um exercício simples para que você possa testar seus conhecimentos. Vamos lá?
- Uma bala é atirada de um canhão e descreve uma parábola de equação: y = 9 x² + 90x. Desta forma, determine a altura máxima atingida pela bala, sabendo que y é a altura em metros e x é o alcance, também em metros.
Resolução:
Como a parábola possui equação y = 9 x² + 90x, certamente sua concavidade está voltada para baixo, e a altura máxima atingida pela bala, corresponde a coordenada y do vértice. Então o vértice é o ponto máximo absoluto. Assim para determinar a altura máxima atingida pela bala, basta determinar o valor y do vértice.
Então:
- a= -9
- b = 90
- c = 0
Portanto, a altura máxima atingida será de 225 metros. Vejamos o cálculo:

Dicas de estudo
Como já falamos no início do nosso post, as funções algébricas são essenciais para o nosso cotidiano. Com certeza você irá se deparar com elas em várias situações da sua vida. Certamente que para quem está se preparando para o vestibular ou para o Enem, esse momento será uma dessas ocasiões.
Então esteja preparado, talvez você já tenha estudado, mas o Guia de Ensino também tem um ótimo material sobre as Funções Algébricas de 1º grau, e muito outros temas da matemática que podem se úteis para se dar bem no exame.
Não deixe de conferir. Até a próxima!


